Project Title : Binomial Heap
Contents
- Title of project
- Introduction to Binomial Heap
- Deliverables
- Technologies used
- End User Documentation
- Online resources
- Team members
- Repository link
Introduction to Binomial Heap
A binomial heap is implemented as a set of binomial trees (compare with a binary heap, which has a shape of a single binary tree), which are defined recursively as follows:
A Binomial Tree of order 0 has 1 node. A Binomial Tree of order k can be constructed by taking two binomial trees of order k-1 and making one as leftmost child or other.
A Binomial Tree of order k has following properties.
- It has exactly 2k nodes.
- It has depth as k.
- There are exactly kCi nodes at depth i for i = 0, 1, . . . , k.
- The root has degree k and children of root are themselves Binomial Trees with order k-1, k-2,.. 0 from left to right.
Because of its unique structure, a binomial tree of order k can be constructed from two trees of order k−1 trivially by attaching one of them as the leftmost child of the root of the other tree. This feature is central to the merge operation of a binomial heap, which is its major advantage over other conventional heaps.
Deliverables
The project delivers the following functionalities via binomial heap as an api to the user :
| Function | Syntax | Parameters | Description | Complexity |
|---|---|---|---|---|
| Create Node | create_node(x) | init a node with key x | returns pointer of newly created Node | O(1) |
| Search Key | search_element(H,x) | key x to search in heap H | returns pointer of key x | O(log(n)) |
| Insert | insert(H,x) | Heap pointer ,pointer to the key to insert | insert a key x to heap H | O(log(n)) |
| Delete | delete_key(H,x) | Heap pointer, key to delete | deletes the key x from the heap H | O(log(n)) |
| Extract Minimum | extract_min_node(H) | Heap pointer | delete and return minimum element in the heap H | O(log(n)) |
| Decrease Key | decrease_key(H,x,y) | Heap pointer, key to be modified, new value to update | decreases the key x by value y in Heap H | O(log(n)) |
| Merge | union_of_heaps(H1,H2) | heap pointers to merge | merges the 2 heaps H1 and H2 and returns pointer to merged heap | O(log(n)) |
Along with above mentioned functionalities, this projects aims to provide comparative analysis on below major operations with that of AVL tree:-
- Insertion
- Deletion
- Search
Also, we have implemented Prim's Algorithm using Binomial heap.The basic method to finding a Minimum Spanning Tree is based on a greedy approach. From a particular vertex, the next vertex is so chosen so that it can be connected to the current tree
using the edge of the lowest weight. Repeating this process until all the nodes are included yields the Minimum Spanning Tree. The Prim’s Algorithm is based on the above approach. It uses a Heap for finding the next vertex with the minimum edge weight which can be included in the Minimum spanning tree.
Technologies used
| Title | Details |
|---|---|
| Languages | C, C++, Python, Markdown |
| Tools | Sublime Text, Git |
End User Documentation
Binomial heap functionalities implementation:-
- go to directory of project and simply run
g++ -o binomial binomialheap.cppcommand through terminal. - The corresponding .out will be generated. Execute this file using the command
./binomial. - A menu will be prompted requesting for the operation to be performed.
Press 1 to insert. Then provide the value to be inserted in the binomial heap.Press 2 to extract min. Returns the minimum value present in the the binomial heap.Press 3 to decrease key. Terminal will prompt for old key. Provide the old key following with the new key(It should be smaller than the old key).Old key will be replaced with the new key(smaller value). If the new value is greater than the old value, then the program will show the error message.Press 4 to deletea value from the binomial heap and then provide the value to be deleted.Press 5 to quitfrom the menu driven program.Press 6 to printthe binomial heap.
Performance Comparison with AVL tree :-
Time analysis for insertion and deletion in Binomial heap:-
- go to directory of project and simply run
g++ -o comparebinomial comp_analysis.cppcommand through terminal. - The corresponding .out will be generated. Execute this file using the
command ./comparebinomial. - The terminal will prompt for filename:-
There are three input files:-
random.txt- contains around 20,000 random numbers.sorted.txt- contains numbers 1-20,00,000 in increasing order. Provide the filename accordingly.
- The terminal will prompt for the numbers of values to be inserted from the file(Maximum value can be 20,00,000).
- The program will create a binomial heap which contains the number of values that are selected in prior step and data will be from the file that was selected earlier. The same program will delete all the values inserted. At the end, it will show the time taken during insertion and time taken for the deletion of all the elements in the binomial heap.
Time analysis for insertion and deletion in AVL tree:-
- go to directory of project and simply run
g++ -o compareavl avl.cppcommand through terminal. - The corresponding .out will be generated. Execute this file using the command
./compareavl. - The terminal will prompt for filename:-
There are three input files:-
random.txt- contains around 20.000 random numbers.sorted.txt- contains numbers 1-20,00,000 in increasing order. Provide the filename accordingly.
- The terminal will prompt for the numbers of values to be inserted from the file(Maximum value can be 20,00,000).
- The program will create a AVL tree which contains the number of values that are selected in prior step and data will be from the file that was selected earlier. The same program will delete all the values inserted. At the end, it will show the time taken during insertion and time taken for the deletion of all the elements in the AVL tree.
Graph demonstarting the performance analysis for insert, search and delete operations between Binomial Heap and AVL tree:-
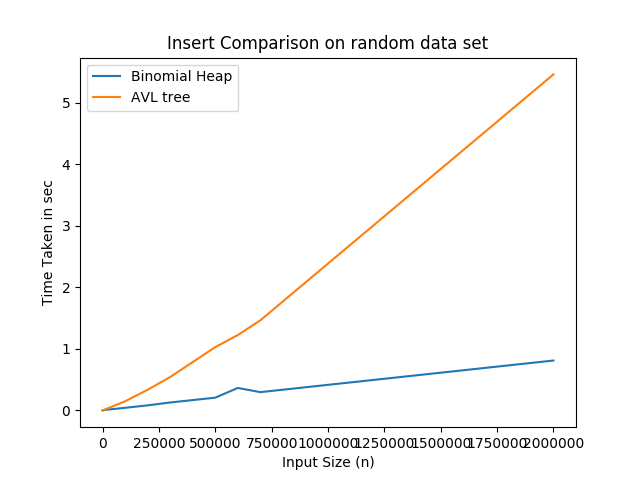
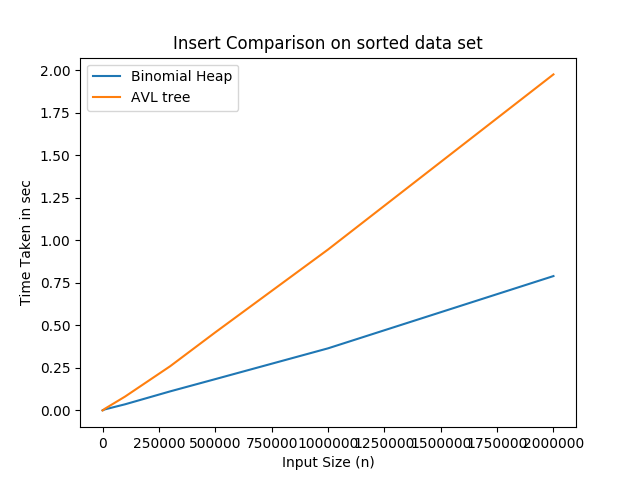
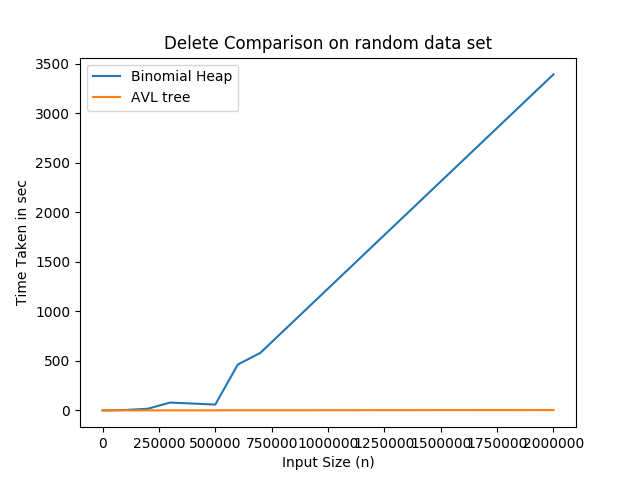
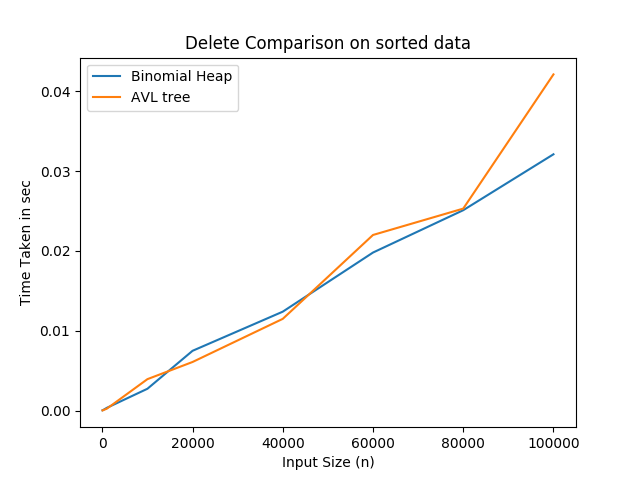
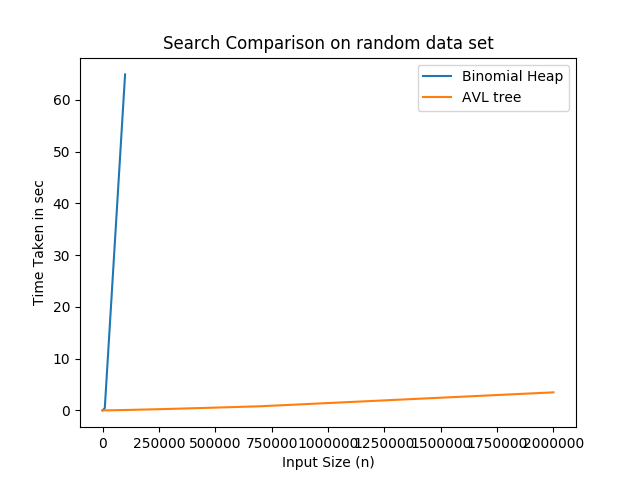
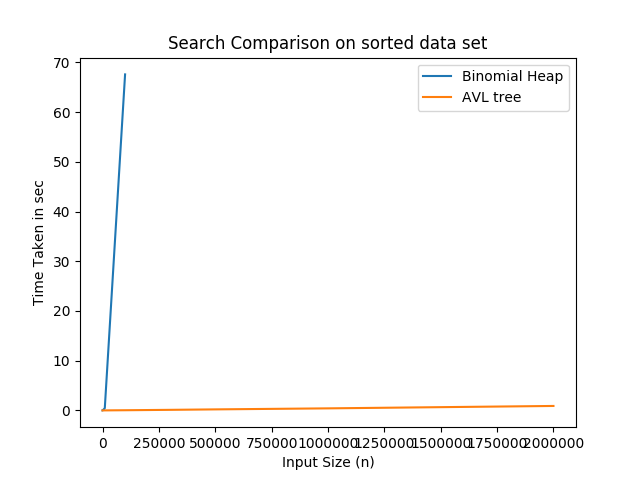
Advantages and Disadvantages of Binomial heap over AVL trees :-
-
Insertion in Binomial heap is faster than the AVL tree. For each insertion in the AVL tree, the new value is compared with multiple nodes until it reaches its desired position in the tree. Unlike AVL tree, insertion operation in Binomial heap first creates a Binomial tree with single key ‘k’, then calls union on Binomial heap H and the new Binomial tree.
-
Searching and Deletion in AVL tree is faster as compared to binomial heap. AVL tree is basically height balanced binary search tree and the number of comparisons required for successful search is limited by the height h and for unsuccessful search is very close to h. Whereas in Binomial heap, the searching is not efficient and may take O(N) time where N is number of nodes.
Implementation of Prim’s Algorithm using Binomial heap :-
In computer science, Prim’s algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.
The algorithm may informally be described as performing the following steps:
- Initialize a tree with a single vertex, chosen arbitrarily from the graph.
- Grow the tree by one edge: of the edges that connect the tree to vertices not yet in the tree, find the minimum-weight edge, and transfer it to the tree.
- Repeat step 2 (until all vertices are in the tree)
To run the Prim’s algorithm using Binomial Heap, follow the steps below
- go to directory of project and simply run
g++ -o prim prims.cppcommand through terminal. - The corresponding .out will be generated. Execute this file using the command
./prim <filename>.
There are two input files:-- prim1.txt - contains a graph information that has 20 vertices and 159 edges.
- prim2.txt - contains a graph information that has 5 vertices and 8 edges.
Input File format:- - First line contains number of vertices followed by number of edges(n).
- There are following n lines that conatins information about edges. Source, destination and weight of the edges.
- Output:-
- The edges that will be present in the Minimum Spanning tree(Format:- Source Destination )
- Weight of the minimum spanning tree
Online resources
Binomial Heaps [Wiki]
Binomial Heaps Overview
cs.toronto.edu
Geeksforgeeks
Fibonacci Heaps [cs.princeton.edu]
Team members
- Shashi Jangra (2018202001)
- Varun Gupta (2018201003)
Repository Link
https://shashijangra22.github.io/Advanced-Problem-Solving-Project/